Aerosol and surface stability of HCoV-19 (SARS-CoV-2) compared to SARS-CoV-1

client for the Study is the US Centers for Disease Control and US Department of Health and Human Services

Full author list

Neeltje van Doremalen, Trenton Bushmaker, Dylan H. Morris, Myndi G. Holbrook, Amandine Gamble, Brandi N. Williamson, Azaibi Tamin, Jennifer L. Harcourt, Natalie J. Thornburg, Susan I. Gerber, James O. Lloyd-Smith, Emmie de Wit, Vincent J. Munster

Content

1 Table of contents:

2 Material and methods page 1-5
3 Supplemental table 1 page 5
4 Supplemental figure 1 and 2 page 6
5 Supplemental figure 3 and 4 page 7
6 Supplemental figure 5 page 8
7 Supplemental references page 8
8 Code and data availability page 9
9 Acknowledgements page 9
10
11
12
13
114 Supplemental methods
15 Laboratory experiments
16 Viruses and titration
17 HCoV-19 nCoV-WA1-2020 (MN985325.1) (Holshue et al., 2020) and SARS-CoV-1 Tor2
18 (AY274119.3) (Marra et al., 2003) were the strains used in our comparison. Viable virus in all surface and
19 aerosol samples was quantified by end-point titration on Vero E6 cells as described previously (van
20 Doremalen et al., 2013).
21 Virus stability in aerosols
22 Virus stability in aerosols was determined as described previously at 65% relative humidity (RH) and
23 21-23°C (Fischer et al., 2016). In short, aerosols (<5 μm) containing HCoV-19 (10 5.25 TCID 50 /mL) or
24 SARS-CoV-1 (10 6.75-7 TCID50/mL) were generated using a 3-jet Collison nebulizer and fed into a Goldberg
25 drum to create an aerosolized environment. Aerosols were maintained in the Goldberg drum and samples
26 were collected at 0, 30, 60, 120 and 180 minutes post-aerosolization on a 47mm gelatin filter (Sartorius).
27 Filters were dissolved in 10 mL of DMEM containing 10% FBS. Three replicate experiments were
28 performed.
29 Virus stability on surfaces
30 Surface stability was evaluated on plastic (polypropylene, ePlastics), AISI 304 alloy stainless steel
31 (Metal Remnants), copper (99.9%) (Metal Remnants) and cardboard (local supplier) representing a variety
32 of household and hospital situations and was performed as described previously at 40% RH and 21-23°C
33 using an inoculum of 10 5 TCID 50 /mL (van Doremalen et al., 2013). This inoculum resulted in cycle-
34 threshold values (Ct) between 20 and 22 similar to those observed in samples from human upper and lower
35 respiratory tract (Zou et al., 2020). In short, 50 μl of virus was deposited on the surface and recovered at
36 predefined time-points by adding 1 mL of DMEM. Stability on cardboard was evaluated by depositing 50
37 μl of virus on the surface and recovering the inoculum by swabbing of the surface, the swab was deposited
38 1 mL of DMEM. Three replicate experiments were performed for each surface.
239 Statistical analyses
40 Bayesian regression model description
41 The durations of detectability depend on initial inoculum and sampling method, as expected. To
42 evaluate the inherent stability of the viruses, we estimated the decay rates of viable virus titers using a
43 Bayesian regression model. This modeling approach allowed us to account for differences in initial
44 inoculum levels across replicates, as well as interval-censoring of titer data and other sources of
45 experimental noise. The model yields estimates of posterior distributions of viral decay rates and half-lives
46 in the various experimental conditions – that is, estimates of the range of plausible values for these
47 parameters given our data, with an estimate of the overall uncertainty (Gelman et al., 2013).
48 In the model notation that follows, the symbol ~ denotes that a random variable is distributed according
49 to the given distribution. Normal distributions are parametrized as Normal(mean, standard deviation).
50 Positive-constrained normal distributions (“Half-Normal”) are parametrized as Half-Normal(mode,
51 standard deviation). We use <Distribution Name>CDF(x, parameters) to denote the cumulative distribution
52 function of a probability distribution, so for example NormalCDF(5, 0, 1) is the value of the Normal(0, 1)
53 cumulative distribution function at 5.
54 Our data consist of 10 experimental conditions: 2 viruses (HCoV-19 and SARS-CoV-1) by 5
55 environmental conditions (aerosols, plastic, stainless steel copper and cardboard). Each has three replicates,
56 and multiple time-points for each replicate. We analyze the two viruses separately. For each, we denote by
57 y ijk the measured log 10 titer in experimental condition i during replicate j at time-point k. To construct our
58 likelihood function, we need to know the probability of observing a given log 10 titer measurement y ijk given
59 values of the parameters.
60 Because our titer data are estimated and recorded in increments of 1/n wells log 10 TCID 50 /mL, where n wells
61 is the number of wells used for endpoint titration, our log 10 titer values are interval-censored – only known
62 to within a range of width 1/n wells . In addition, there is a degree of measurement noise in the titration process
63 itself.
64 To model this, we assume that in each experimental condition i, there is a true underlying log 10 titer
65 x ijk that is measured with some amount of experimental noise or error ε ijk and then observed as an interval-
66 censored value y ijk ≈ x ijk + ε ijk . We model the measurement errors ε ijk as Normally distributed with a standard
67 deviation σ i that is shared by all samples in the given experimental condition, this reflects the fact that some
68 experimental setups may be more or less noisy than others.
369 ε ijk ~ Normal(0, σ i )
70 We model the probability of observing an interval-censored log 10 titer value y ijk given a true underlying
71
log 10 titer x ijk and a measurement error standard deviation σ i as:
72 P(y ijk | x ijk , σ i ) = NormalCDF(y ijk , x ijk , σ i ) – NormalCDF(y ijk – 1/n wells , x ijk , σ i )
73 This reflects the probability given a true value x ijk plus the measurement error x ijk + ε ijk falls between
74 y ijk – 1/n wells and y ijk . Due to the log 10 titer imputation technique used, a titer in that range is most likely to
75 be rounded up and reported as y ijk .
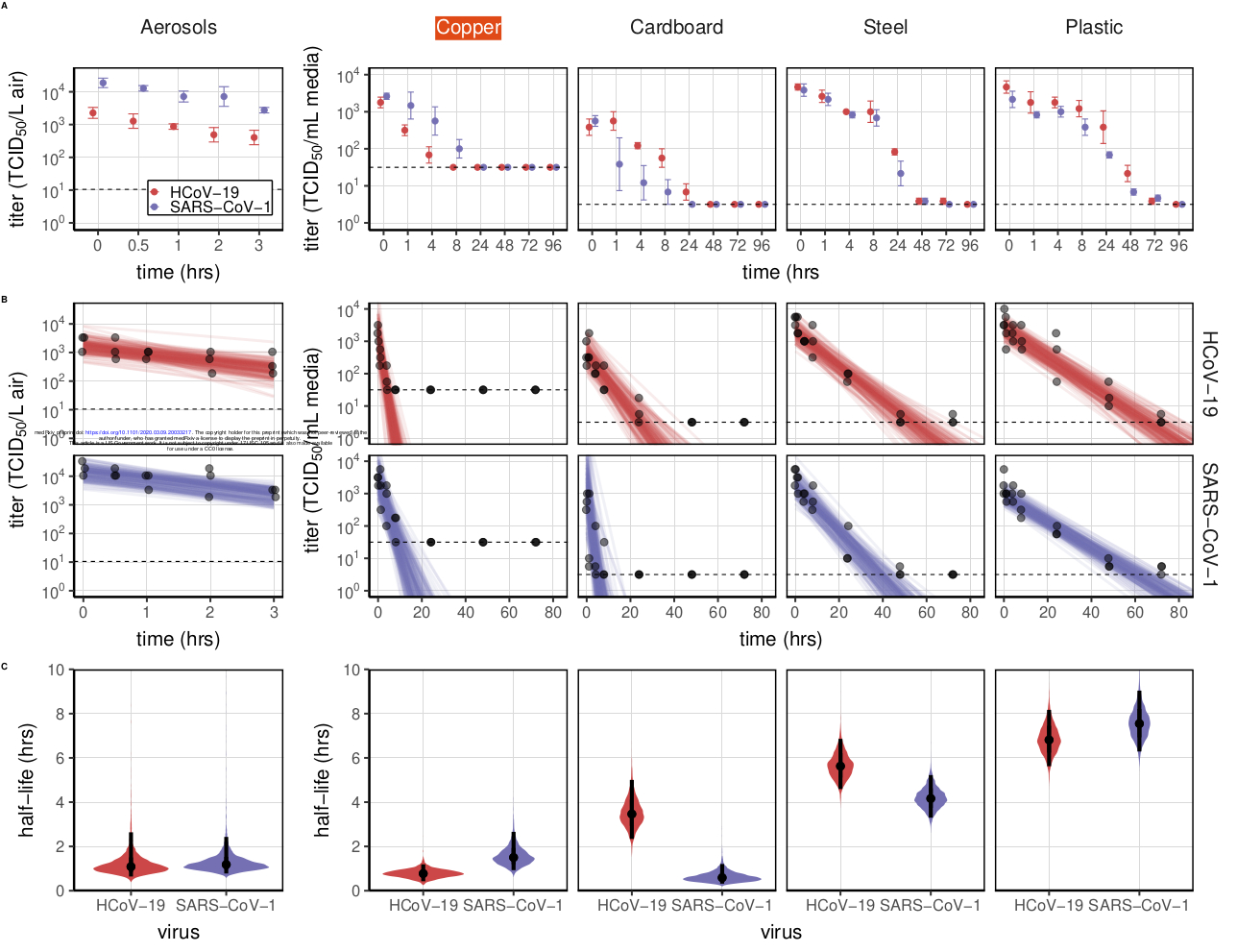
76
77
The detection limit of our experiment is 0.5 log 10 TCID 50 /mL. The probability of observing an
undetectable measured log 10 titer value y ijk given a true log 10 titer value x ijk is given by:
78 P(y ijk ≤ 0.5 | x ijk , σ i ) = NormalCDF(0.5, x ijk , σ i )
79 We then model each replicate j for experimental condition i as starting with some true initial log 10 titer
80 x ij (0) = x ij0 . We assume that viruses in experimental condition i decay exponentially at a rate λ i over time t.
81 It follows that
x ij (t) = x ij0 – λ i t
82
83
84
where t k is the k th measured time-point.
Model prior distributions
85 We place a weakly informative Normal prior distribution on the initial log 10 titers x ij0 to rule out
86 implausibly large or small values (e.g. in this case undetectable log 10 titers or log 10 titers much higher than
87 the deposited concentration), while allowing the data to determine estimates within plausible ranges:
88
89
90
x ij0 ~ Normal(4.5, 2.5)
We likewise placed a weakly informative Half-Normal prior on the exponential decay rates λ i :
λ i ~ Half-Normal(0.5, 4)
4We placed a weakly informative Half-Normal prior on the standard deviations of the experimental
91
92
error distributions σ i :
σ i ~ Half-Normal(0, 2)
93
94
Markov Chain Monte Carlo Methods
95 We drew posterior samples using Stan, which implements a No-U-Turn Sampler (a form of Markov
96 Chain Monte Carlo). We ran four replicate chains from random initial conditions for 2000 iterations, with
97 the first 1000 iterations as a warmup/adaptation period. We saved the final 1000 iterations from each chain,
98 giving us a total of 4000 posterior samples. We assessed convergence by inspecting trace plots and
99 examining R̂ and effective sample size (n eff ) statistics (R̂ for all parameters ≤ 1.003, n eff for all parameters
100 ≥28% of total samples).
101 Supplemental table and figures
102 Table 1. Posterior median estimates and 95% credible intervals (2.5%–97.5% quantile range) for half-lives
103 of HCoV-19 and SARS-CoV-1 in aerosols and on various surfaces, as well as a median estimate and 95%
104 credible interval for the difference between the two half-lives (HCoV-19 – SARS-CoV-1).
HCoV-19 SARS-CoV-1 HCoV-19 – SARS-CoV-1
half-life (hrs) half-life (hrs) difference (hrs)
Material median 2.5% 97.5% median 2.5% 97.5% median 2.5% 97.5%
Aerosols 1.09 0.64 2.64 1.18 0.778 2.43 -0.0913 -1.35 1.39
Copper 0.774 0.427 1.19 1.5 0.929 2.66 -0.735 -1.91 -0.0339
Cardboard 3.46 2.34 5 0.587 0.317 1.21 2.85 1.58 4.41
Steel 5.63 4.59 6.86 4.16 3.3 5.22 1.46 0.00127 2.96
Plastic 6.81 5.62 8.17 7.55 6.29 9.04 -0.722 -2.64 1.16
105
106 Figures S1–S5 (below) show Bayesian fits to individual replicate virus decay data for each virus. Replicates
107 are shown in panel columns, viruses in panel rows. Lines are 50 random draws per panel from the posterior
5108 distribution of fitted lines, to show level of uncertainty. Time axis is shown out to the latest time taken to
109 reach an undetectable titer in the considered experimental conditions.
110
111 Figure S1. Individual replicate fits for aerosols. Columns show replicates, rows show virus (HCoV-19
112 above, SARS-CoV-1 below). Lines are 50 random draws per panel from the posterior distribution of fitted
113 lines, to show level of uncertainty.
114
115 Figure S2. Individual replicate fits for plastic. Columns show replicates, rows show virus (HCoV-19 above,
116 SARS-CoV-1 below). Lines are 50 random draws per panel from the posterior distribution of fitted lines,
117 to show level of uncertainty.
6118
119 Figure S3. Individual replicate fits for steel. Columns show replicates, rows show virus (HCoV-19 above,
120 SARS-CoV-1 below). Lines are 50 random draws per panel from the posterior distribution of fitted lines,
121 to show level of uncertainty.
122
123 Figure S4. Individual replicate fits for copper. Columns show replicates, rows show virus (HCoV-19 above,
124 SARS-CoV-1 below). Lines are 50 random draws per panel from the posterior distribution of fitted lines,
125 to show level of uncertainty. Fits are substantially poorer for SARS-CoV-1 than for HCoV-19, and data do
126 not follow a linear downward trend over time, suggesting that the difference in observed decay rates should
127 be interpreted with caution.
7128
129 Figure S5. Individual replicate fits for cardboard. Columns show replicates, rows show virus (HCoV-19
130 above, SARS-CoV-1 below). Lines are 50 random draws per panel from the posterior distribution of fitted
131 lines, to show level of uncertainty. Fits are substantially poorer for SARS-CoV-1 than for HCoV-19, and
132 data do not follow a linear downward trend over time, suggesting that the difference in observed decay rates
133 should be interpreted with caution.
134 Supplemental references
135 Fischer, R.J., Bushmaker, T., Judson, S., Munster, V.J., 2016. Comparison of the Aerosol Stability of 2
136 Strains of Zaire ebolavirus From the 1976 and 2013 Outbreaks. J. Infect. Dis. 214, 290–293.
137
138
139
Gelman, A., Carlin, J.B., Stern, H.S., Dunson, D.B., Vehtari, A., Rubin, D.B., 2013. Bayesian Data
Analysis, Third Edition. CRC Press.
Holshue, M.L., DeBolt, C., Lindquist, S., Lofy, K.H., Wiesman, J., Bruce, H., Spitters, C., Ericson, K.,
140 Wilkerson, S., Tural, A., Diaz, G., Cohn, A., Fox, L., Patel, A., Gerber, S.I., Kim, L., Tong, S., Lu,
141 X., Lindstrom, S., Pallansch, M.A., Weldon, W.C., Biggs, H.M., Uyeki, T.M., Pillai, S.K., 2020.
142 First Case of 2019 Novel Coronavirus in the United States. N. Engl. J. Med. 382, 929–936.
143 Marra, M.A., Jones, S.J.M., Astell, C.R., Holt, R.A., Brooks-Wilson, A., Butterfield, Y.S.N., Khattra, J.,
144 Asano, J.K., Barber, S.A., Chan, S.Y., Cloutier, A., Coughlin, S.M., Freeman, D., Girn, N., Griffith,
145 O.L., Leach, S.R., Mayo, M., McDonald, H., Montgomery, S.B., Pandoh, P.K., Petrescu, A.S.,
146 Robertson, A.G., Schein, J.E., Siddiqui, A., Smailus, D.E., Stott, J.M., Yang, G.S., Plummer, F.,
147 Andonov, A., Artsob, H., Bastien, N., Bernard, K., Booth, T.F., Bowness, D., Czub, M., Drebot, M.,
148 Fernando, L., Flick, R., Garbutt, M., Gray, M., Grolla, A., Jones, S., Feldmann, H., Meyers, A.,
8149 Kabani, A., Li, Y., Normand, S., Stroher, U., Tipples, G.A., Tyler, S., Vogrig, R., Ward, D., Watson,
150 B., Brunham, R.C., Krajden, M., Petric, M., Skowronski, D.M., Upton, C., Roper, R.L., 2003. The
151 Genome sequence of the SARS-associated coronavirus. Science 300, 1399–1404.
152 van Doremalen, N., Bushmaker, T., Munster, V., 2013. Stability of Middle East respiratory syndrome
153 coronavirus (MERS-CoV) under different environmental conditions. Eurosurveillance 18, 20590.
154 Zou, L., Ruan, F., Huang, M., Liang, L., Huang, H., Hong, Z., Yu, J., Kang, M., Song, Y., Xia, J., Guo,
155 Q., Song, T., He, J., Yen, H.-L., Peiris, M., Wu, J., 2020. SARS-CoV-2 Viral Load in Upper
156 Respiratory Specimens of Infected Patients. N. Engl. J. Med. In press.
157
158
Code and data availability
Code and data to reproduce the Bayesian estimation results and produce corresponding figures are
159 archived online at OSF: <insert link> and available on Github: <insert link>
160 Acknowledgements
161 We would like to thank Kwe Claude Yinde and Michael Letko for experimental assistance. This
162 research was supported by the Intramural Research Program of the National Institute of Allergy and
163 Infectious Diseases (NIAID), National Institutes of Health (NIH). JOL-S and AG were supported by the
164 Defense Advanced Research Projects Agency DARPA PREEMPT # D18AC00031, and JOL-S was
165 supported by the U.S. National Science Foundation (DEB-1557022) and the Strategic Environmental
166 Research and Development Program (SERDP, RC‐2635) of the U.S. Department of Defense. The findings
167 and conclusions in this report are those of the author(s) and do not necessarily represent the official position
168 of the Centers for Disease Control and Prevention. Names of specific vendors, manufacturers, or products
169 are included for public health and informational purposes; inclusion does not imply endorsement of the
170 vendors, manufacturers, or products by the Centers for Disease Control and Prevention or the US
171 Department of Health and Human Services.